边缘提取
描述信号突变
对信号求导,x方向上,有
∂x∂f(x,y)=ϵ→0limϵf(x+ϵ,y)−f(x,y)
可以用差分来近似替代
∂x∂f(x,y)≈1f(x+1,y)−f(x,y)=f(x+1,y)−f(x,y)
从而可以化为卷积的操作,卷积模板为:[−11]
同理,y方向上的模板为[−11]或[1−1]
也可以定义为f(x+1,y)−f(x−1,y),这样卷积模板就变成了[−101]
图像的梯度∇f=[∂x∂f,∂y∂f]

梯度方向,指向信号变化最大的方向。方向通常与边的方向垂直。
∥∇f∥称为梯度幅值(Gradient Magnitude)
几种典型算子
Prewitt算子
Mx=−1−1−1000111My=10−110−110−1
拿x方向来看,相比于[−11],好处是将上面和下面的点一起加入比较,减少噪声造成的影响。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| import cv2
import numpy as np
img = cv2.imread('img_set/miku.jpg')
prewittx = np.array([[-1, 0, 1],
[-1, 0, 1],
[-1, 0, 1]])
prewitty = np.array([[1, 1, 1],
[0, 0, 0],
[-1, -1, -1]])
dst1 = cv2.filter2D(img, -1, prewittx)
dst2 = cv2.filter2D(img, -1, prewitty)
cv2.imshow('original', img)
cv2.imshow('convx', dst1)
cv2.imshow('convy', dst2)
cv2.waitKey(0)
cv2.destroyAllWindows()
|
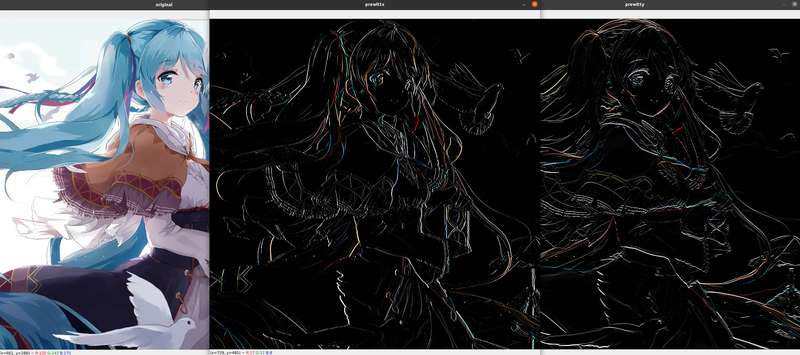
Soble算子
Mx=−1−2−1000121My=10−120−210−1
Sobel算子相当于在提取边缘之前,先对图像做了一次高斯滤波,然后再提取边缘。这样对噪声的敏感程度会更低一些。
Mx=−1−2−1000121=121[−101]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
soblex = np.array([[-1, 0, 1],
[-2, 0, 2],
[-1, 0, 1]])
sobley = np.array([[1, 2, 1],
[0, 0, 0],
[-1, -2, -1]])
dst3 = cv2.filter2D(img, -1, prewittx)
dst4 = cv2.filter2D(img, -1, prewitty)
cv2.imshow('soblex', dst3)
cv2.imshow('sobley', dst4)
cv2.waitKey(0)
cv2.destroyAllWindows()
|
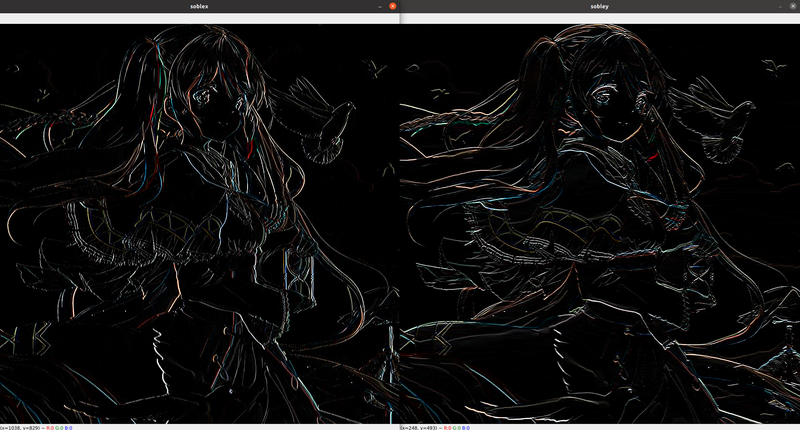
Roberts算子
Mx=[0−110]My=[100−1]
衡量的是斜对角方向的差异值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
robertsx = np.array([[0, 1],
[-1, 0]])
robertsy = np.array([[1, 0],
[0, -1]])
dst5 = cv2.filter2D(img, -1, robertsx)
dst6 = cv2.filter2D(img, -1, robertsy)
cv2.imshow('robertsx', dst5)
cv2.imshow('robertsy', dst6)
cv2.waitKey(0)
cv2.destroyAllWindows()
|
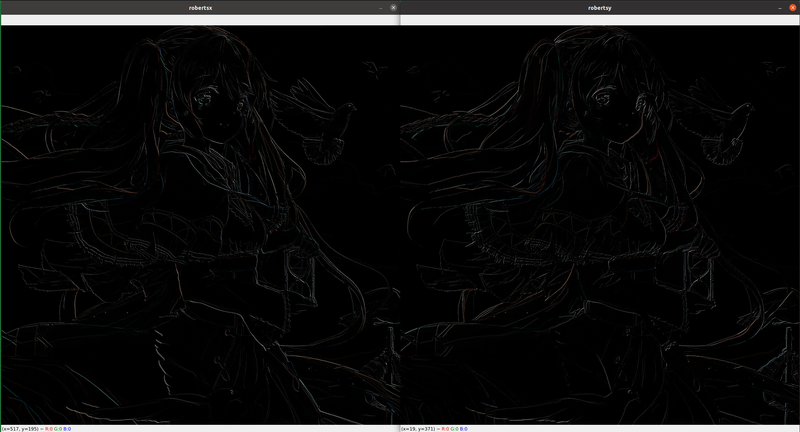
高斯偏导核
图像有噪声怎么办?
- 平滑,去躁
- 对平滑的结果进行求导
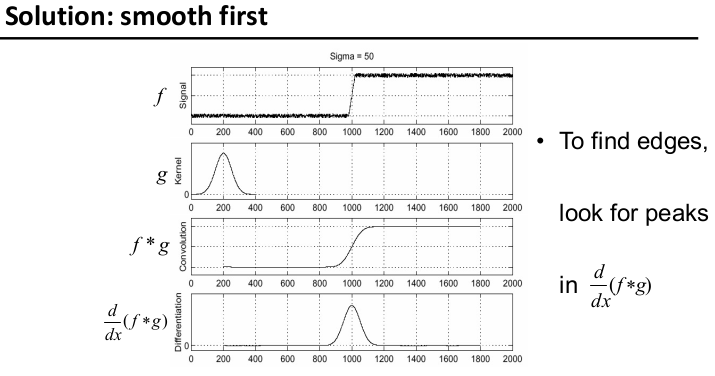
但是,卷积的操作是比较耗时的,先平滑再求导,相当于做了两次连续卷积。能不能一次卷积就可以得到结果呢?
由之前的知识可知,卷积具有交换律和结合律,因此
dxd(f∗g)=f∗dxdg
高斯核变成了高斯偏导核(Derivative of Gaussian filter)
高斯偏导模板是不可分离的,对高斯核求导就可以看出(高斯核里的x和y是二次的,求导之后会变成一次的,无法分离出x和y)。
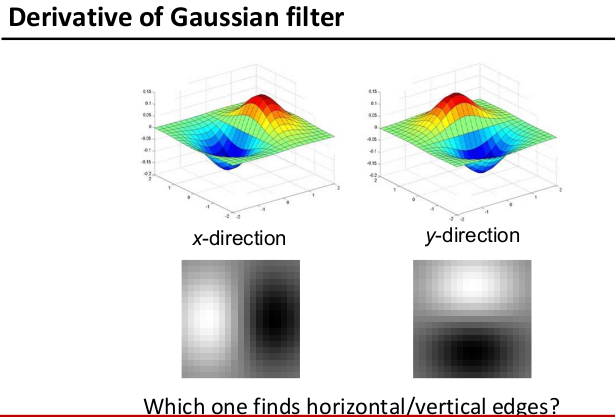
高斯平滑核和高斯偏导核对比
高斯平滑核:移除“高频”信号;没有负数;加权求和后为1。
高斯偏导核:用来提取边缘信息;里面的值可以为负数;加权求和为0;值越高,代表越有可能是边缘。
Canny算子
论文下载:A Computational Approach to Edge Detection
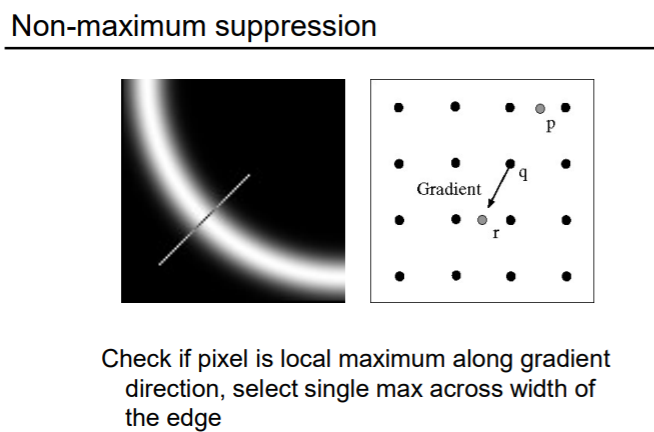
非最大化抑制(Non-Maximum Suppression)
把很宽的边处理成窄边,真正的找到边的中点。
q点在梯度方向上与邻居p和r(p和r离q都只有一个像素)比较,保留梯度值大的那个点。通过q算出来的要与之比较的p和r有可能不在整数位置上,这时候可以用其周围的四个像素进行“双线性插值”求出像素点p和r的位置。
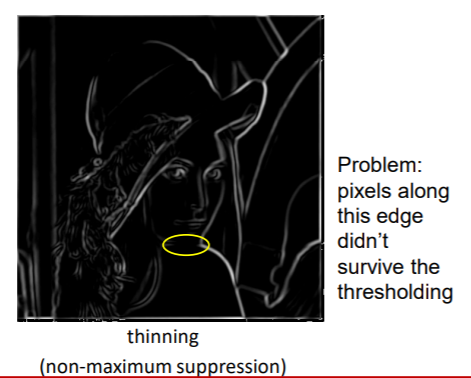
门限化
门限(阈值)如果设置的较高,会使一些真正的边“消失”;如果设置的较低,很多“假边”又会出来。
双门限化(Hysteresis Thresholding)
Canny算子做的工作是,先用高门限,把强边缘检测出来。然后降低门限,把响应值比较低的边也显现出来。假设“噪声边不会与强边缘有连接关系”,只有与强边缘有连接关系的边才是真正的边。
将强边缘与弱边缘叠加,并删除与强边缘没有连接关系的弱边缘。

算法流程:
- 用高斯偏导核对图像滤波
- 找到幅值最大的点和梯度方向
- 非最大化抑制
- 连接和门限化(hysteresis)
- 定义高低两个门限
- 用高门限去找到强边缘,用低门限把有连接关系的边找回来
该算法于1986年发表于人工智能领域顶级期刊 Pattern Analysis and Machine Intelligence(PAMI)上










