李宏毅机器学习笔记

课程地址：http://speech.ee.ntu.edu.tw/~tlkagk/courses_ML17_2.html

Lecture 0-1： Introduction of Machine Learning

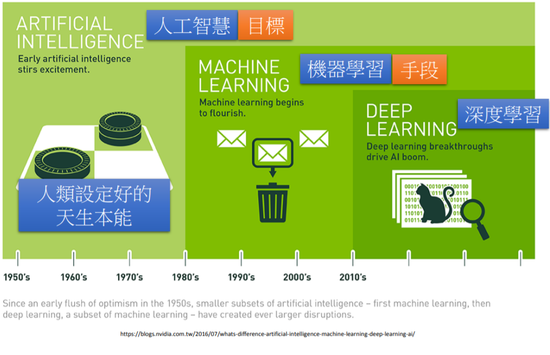
人工智能是目标，机器学习是手段，深度学习是机器学习的一种方法

人工智能还是人工智障？

图片来源：http://www.commitstrip.com/en/2017/06/07/ai-inside/

什么是机器学习？

机器学习的步骤

• 1.define a set of function

• 2.goodness of function

• 3.pick the best function

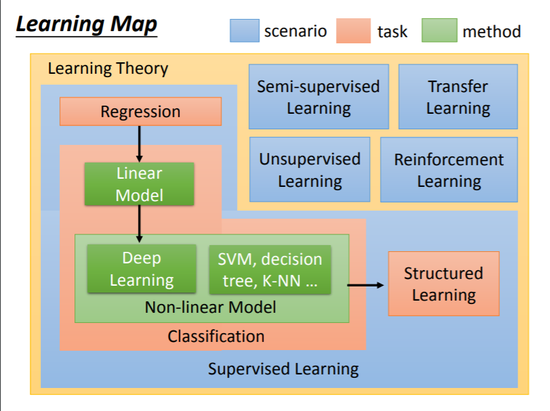
半监督学习：既包含有label的数据又包含无label的数据

迁移学习：跟我们现在考虑的问题没什么特别联系

无监督学习：完全无label

Structured Learning

增强学习：AlphGo里有用到。机器所拥有的只有一个分数，从评价中去学习。

Regression

回归可以做什么？

股票预测、无人驾驶、推荐等

举例：预测宝可梦进化后的CP值
每只宝可梦，都有cp，hp，种类，重量，身高等属性

线性回归

---

损失函数

input：进化前的CP值，用$x_{cp}$表示
output：进化后的cp值，用$y$表示

假设函数为$y = b + w \times x_{cp}$，其中，$w$和$b$未知，是算法要学习得到的。

线性函数定义：

$$y = b + \sum_{i=1}^n w_i x_i$$

$x$是特征（如宝可梦的cp值就是特征），$w$是权重，$b$是偏置值。上式中就假设有$n$个特征。

注意，$x_i$表示第$i$个特征，$x^1$表示数据集中的第1个样本

假设有10只宝可梦作训练集

$(x^1,\hat{y}^1) \\ (x^2,\hat{y}^2) \\ \vdots \\ \vdots \\ (x^{10},\hat{y}^{10})$

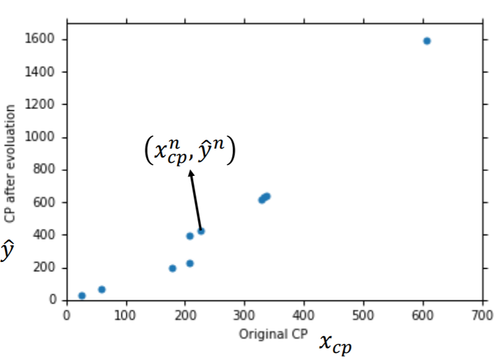
loss function：损失函数，又叫cost function
可定义为：

$$L(w,b) = \sum_{n=1}^{10} {\big(\hat{y}^n - (b+w\times x_{cp}^n)\big)}^2$$

至于为什么用差的平方累加定义，吴恩达的机器学习课程中已经用最大似然估计给出了推导。

//TODO 补充推导过程

目标：找到一组$w$和$b$，使得L的值最小
方法：很多种，现在学习梯度下降（Gradient Descent）

梯度下降的过程

• 随机选取一个初始的点$w^0$,$b^0$

• 做如下循环，直到收敛

  $w^{i+1} = w^i - \eta \frac{\partial L}{\partial w}\mid_{w = w^i,b = b^i}$

  $b^{i+1} = b^i - \eta \frac{\partial L}{\partial b}\mid_{w = w^i,b = b^i}$

其中，$\eta$叫做学习速率

上式中所有不同的参数对$L$的偏微分可记为

$$\nabla L = \begin{bmatrix} \frac{\partial L}{\partial w} \\ \frac{\partial L}{\partial b} \end{bmatrix}$$

即梯度（gradient）

用numpy模拟梯度下降的过程，代码如下

gradient descent demo1

gradient descent demo2

---

正则化

过拟合的解决方法：

1.增加数据
2.特征选择
3.正则化

加入正则化参数防止过拟合

$$L = \sum_{n} {\big(\hat{y}^n - (b+\sum_{}w_i x_i) \big)}^2 + \lambda \sum (w_i)^2$$

---

模型的误差及如何选取合适的模型

关于模型的评价及如何选取合适的模型，在《机器学习中学习曲线的bias vs variance以及数据量m》这篇文章里已经讲得很详细了，看不懂李宏毅老师讲的的可以来这里充电。

Classification

分类可以做什么？

信用评估、医疗诊断、手写数字识别

仍然以宝可梦为例

$$f(x_1) = electric$$

$$f(x_2) = water$$

$$f(x_3) = grass$$

方法

Function(model):

g(x) > 0   output = class 1
else       output = class 2

Loss function:

$$L(f) = \sum_n \delta(f(x^n) \neq \hat{y^n})$$

该function无法微分，怎么解决呢？

Perceptron（感知机）和SVM（支持向量机）

留到后面讲，现在用朴素贝叶斯的方法。

总共有800只宝可梦，将宝可梦图鉴里前400只用作training data，后400只用作testing data。以水系和一般系为例，解决二元分类问题。

Training: 79 Water(C1),61 Normal(C2)

$P(C_1) = \frac{79}{79 + 61} = 0.56$

$P(C_2) = \frac{61}{79 + 61} = 0.44$

$P(x | C1) = ?$