课程地址：https://www.bilibili.com/video/BV1nz4y197Qv

课件地址：https://github.com/CV-xueba/A01_cvclass_basic

卷积

定义

ff是图像的矩阵，gg是卷积核（一个n×nn \times n的矩阵）。
卷积f∗gf*g的数学表达式为：

(f∗g)[m,n]=∑k,lf[m−k,n−l]g[k,l](f*g)[m,n] = \sum_{k,l}f[m-k,n-l]g[k,l]

其中m和n是中心点的坐标。

对图像卷积一次的结果，是一个实数

  1. 将卷积核“翻转”
  2. 图像与卷积核对应值相乘并求和
  3. 循环直到图像卷积完成

卷积的性质

卷积的效果

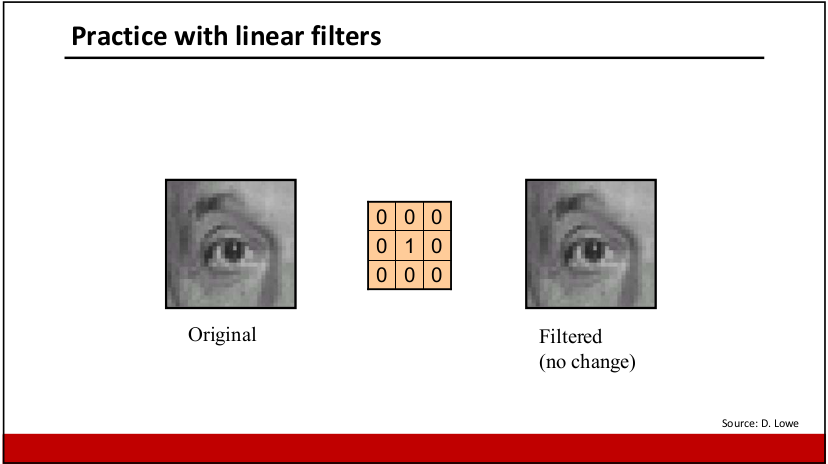
  1. 不变

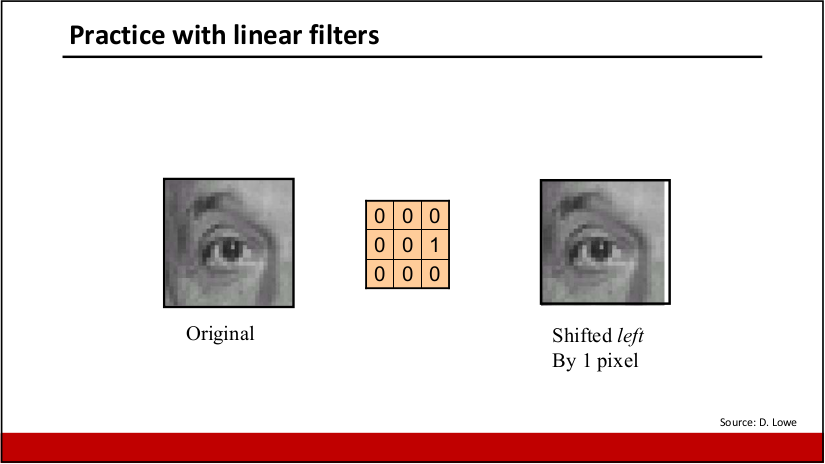
  1. 左移

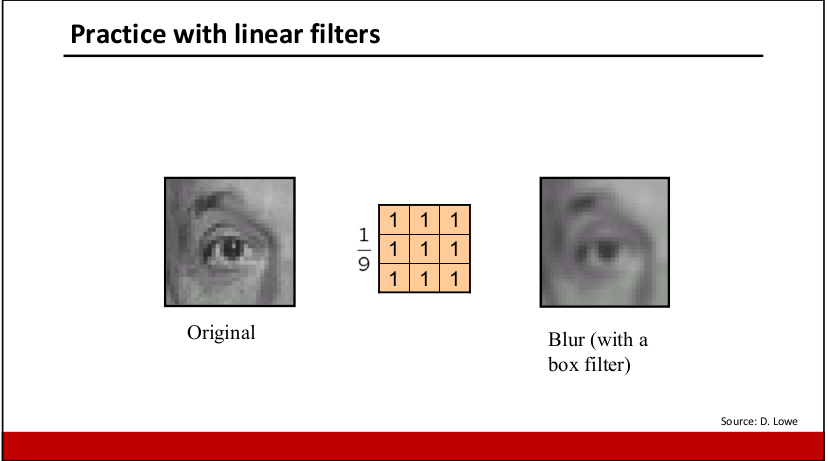
  1. 平滑（去燥）

  1. 锐化

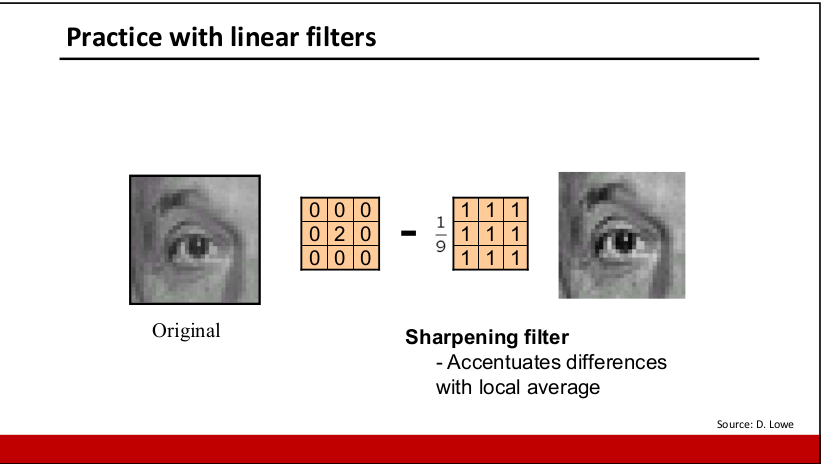
原理：

I是原图，e是脉冲模板（如1所示）

I∗e−I∗g=I∗(e−g)I∗(e−g)+I∗e=I∗(2e−g)\begin{gathered} I*e - I*g = I*(e - g) \\ I*(e - g) + I*e = I*(2e - g) \end{gathered}

高斯平滑核

用19[111111111]\frac{1}{9} \begin{bmatrix} 1 & 1 & 1\\ 1 & 1 & 1\\ 1 & 1 & 1 \end{bmatrix} 当卷积核去平滑图像会产生“振铃”效果，因为该卷积核将离中心距离不同的点按相同的权重对待（都是1），我们更希望它的权值模板能按照距离的远近处理，这就引入了高斯核（Gaussian Kernel）。

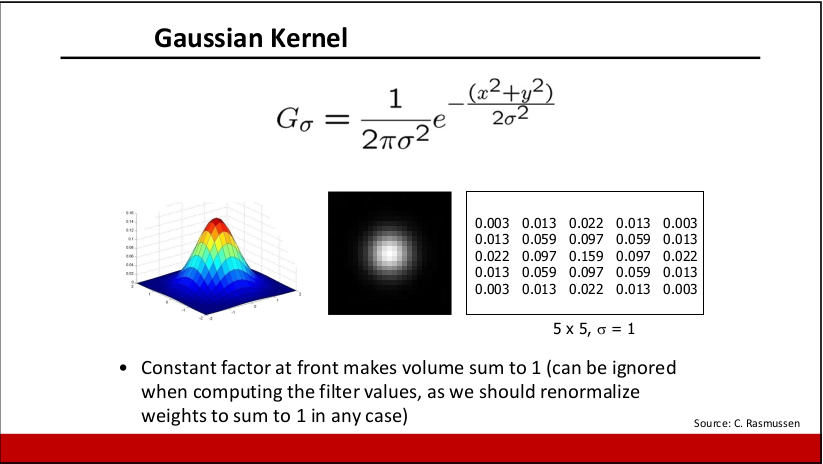
这里我们要求对每个元素加权后归一，即∑g=1\sum g = 1

注意，高斯核是一个对称阵。

重要性质

使用一个方差为σ12\sigma_1^2的高斯核与图像做卷积，再与一个方差为σ22\sigma_2^2的高斯核再一次卷积，等同于原图像与一个方差为σ12+σ22\sqrt{\sigma_1^2 + \sigma_2^2}的高斯核做一次 卷积。

高斯核分解

Gσ(x,y)=12πσ2exp⁡−x2+y22σ2=(12πσexp⁡−x22σ2)(12πσexp⁡−y22σ2)\begin{aligned} G_\sigma(x,y) &= \frac{1}{2 \pi \sigma^2} \exp^{-\frac{x^2 + y^2}{2 \sigma^2}}\\ &=\bigg(\frac{1}{\sqrt{2 \pi \sigma}} \exp^{-\frac{x^2}{2 \sigma^2}}\bigg) \bigg(\frac{1}{\sqrt{2 \pi \sigma}} \exp^{-\frac{y^2}{2 \sigma^2}}\bigg) \end{aligned}

分解的主要应用是加速卷积的过程。

一个n×nn \times n的图像用m×mm \times m的核区卷积。暴力解法的时间复杂度：O(n2m2)O(n^2 m^2)

将高斯核分解后，时间复杂度：O(n2m)O(n^2 m)

去噪

噪声分类

椒盐噪声（Salt-and-pepper）
脉冲噪声（Impulse noise）
高斯噪声（Gaussian noise）

滤波

高斯滤波器（Gaussian filtering）

第一行是灰度图分别叠加了不同大小N(0,σ)N(0,\sigma)的高斯分布之后的噪声图像。

第二行和第三行是用不同σ\sigma的高斯核进行滤波的结果。

σ=1\sigma = 1时，滤波模板的大小是7×77 \times 7（根据3σ3\sigma法则，左边3右边3加中间1），σ=2\sigma = 2时，滤波模板大小是13×1313 \times 13（左边6右边6加中间1）

可以看到，对于噪声比较小的（例如σ=0.05\sigma = 0.05），可以用一个小的滤波模板即可将其恢复为原来的灰度图；对于噪声大的，要用大的滤波模板才能恢复。但是大模板会造成边缘更加平滑，使轮廓信号衰减，造成图像“模糊”。

但是对于椒盐噪声，用高斯滤波器却无法得到好的效果。

中值滤波器（Median filtering）

中值滤波器：找中位数，是一个非线性的滤波器。

滤波的效果：对椒盐噪声特别有效。

即使是中值滤波，大模板也会导致图像“模糊”。

锐化

原理

数学描述：

f+α(f−f∗g)=(1+α)f−αf∗g=f∗((1+α)e−αg)\begin{aligned} f + \alpha(f - f*g) &= (1 + \alpha)f - \alpha f*g\\ &= f*((1 + \alpha)e - \alpha g) \end{aligned}