总览

如果我们知道所有属于某条线上的所有点，可以使用最小二乘的方法。
如果不属于该线上的点（噪声点）比较多，可以使用RANSAC方法。
如果有很多线，其他线对于我取某条线来说都是噪声，可以用RANSAC或者Hough transform的思想。
线都不确定，snake（蛇形模型）

最小二乘（Least squares）

许多机器学习的入门课程都有关于最小二乘的详细描述，老师在这里使用的是 正规方程（Normal Equation）来解决该问题。当然，还有其他方法比梯度下降等，请参考机器学习等相应教材。

当线垂直 $x$ 轴的时候的时候，最小二乘无法使用。这时候需要将点沿纵轴方向到线的距离改为点到直线的距离，这就是全最小二乘（Total Least Squares）

极大似然估计与全最小二乘

我们可以将点到直线的距离，看成均值为0，方差为 $\sigma^2$ 的正态分布。

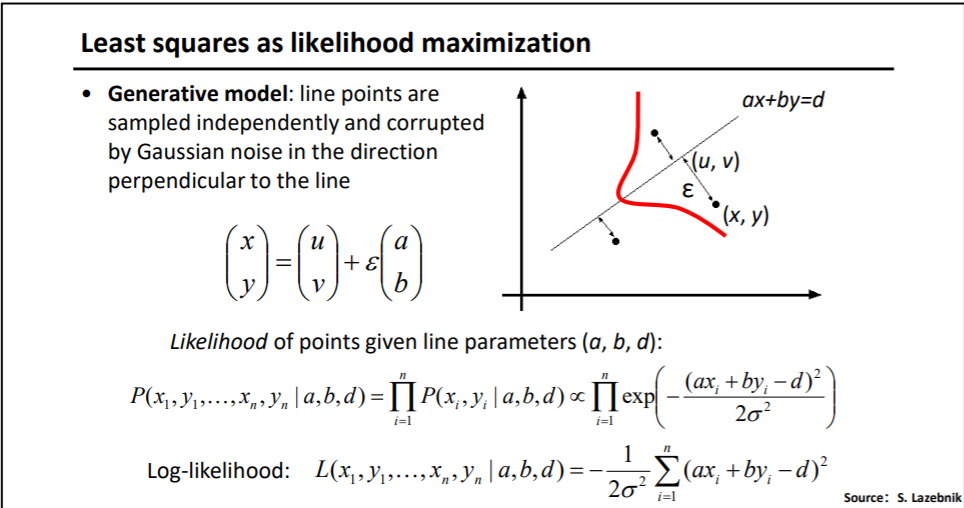
这样就将误差函数转换成了概率的形式。然后就可以用极大似然估计求解。

这是一种很重要的思想，即一个事情可以有多种方式去建模。

鲁棒估计

在用全最小二乘拟合曲线的过程中，当数据中有一些很大的噪声，导致个别点偏离正确模型非常远时（将这种点称为“外点（outliers）”），该点对最终拟合出来的曲线影响较大。鲁棒估计（Robust estimators）不再将点到直线的距离直接作为要减小的误差，而是将该距离 $u$ 输入函数 $\rho(u;\sigma) = \frac{u^2}{\sigma^2 + u^2}$ ，把输出当做要减小的误差。

这样一来总的误差为

$E = \sum_{i=1}^n \rho(r_i(x_i,\theta);\sigma)$

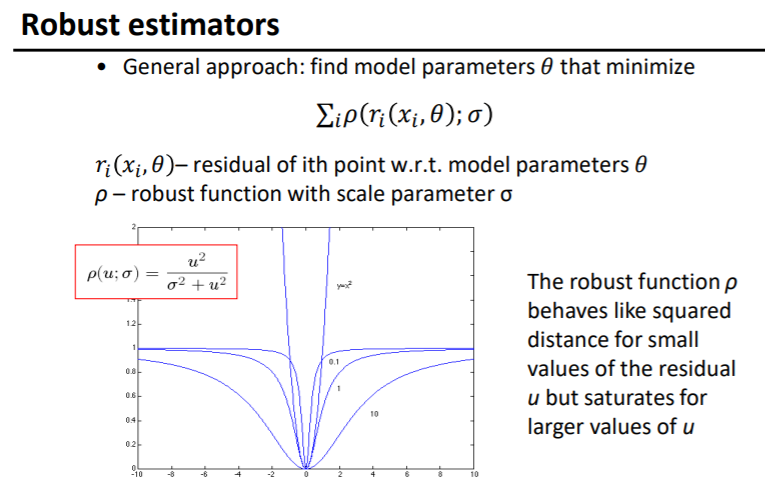
看一下效果：

注意，这是一个非线性的优化问题。

随机采样一致性（RANSAC）

从数据中采集最小子集（最小子集的大小由所研究的问题决定，如拟合直线，则最小子集数目为2，因为两点确定一条直线），然后用这个最小子集拟合一条直线 $l_i$ （得到 $\tilde{H}$ ）；
.计算每个点到直线 $l_1$ 的距离（在拟合直线的情况下，我采用的是点 $x_i$ 通过 $\tilde{H}$ 得到的 $\tilde{y_i} = \tilde{H}x_i$ 与真值的差的绝对值 $|y_i - \tilde{y_i}|$ ），如果 $d_{\bot} < t$ ， $t$ 是距离阈值，则记为“内点（inlier）”。统计本次得到的内点的数目 $n_i$ 。如果 $n_i > T$ ， $T$ 是内点数目阈值，则说明当前所估计的 $\tilde{H}$ 足够好，利用这些内点再重新估计 $\tilde{H}$ ，然后返回 $\tilde{H}$ ，退出。否则返回（1）继续执行。

作者：Kissrabbit
链接：https://zhuanlan.zhihu.com/p/34676804
来源：知乎