CV学习系列：SIFT

写在前面

尺度不变特征变换（Scale-invariant feature transform, SIFT）

论文：Distinctive Image Features from Scale-Invariant Keypoints

你们能理解那种感受吗？就是，我明明正在实验室听b站的up主讲SIFT，却还要担心老板会进来…

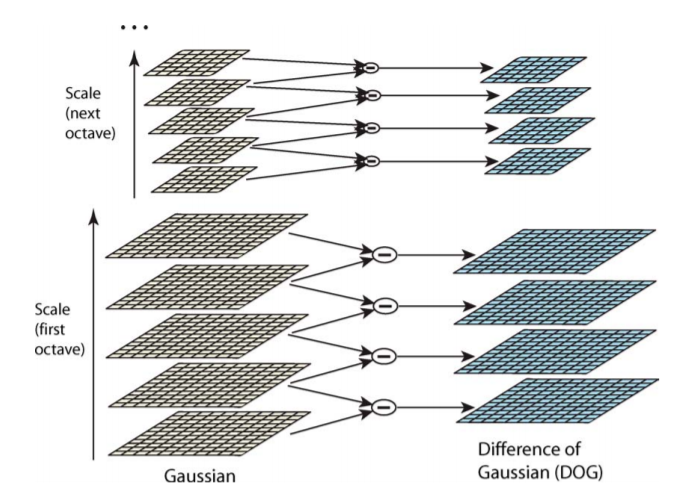
高斯差分金字塔

octave：组

高斯金字塔（尺度空间）：

• 用不同大小（尺度）的$\sigma$的高斯核对原图片卷积得octave1，对octave1进行降采样得到octave2

• 用不同大小（尺度）的$\sigma$的高斯核卷积对octave2卷积，接着降采样得到octave3

• 用不同大小（尺度）的$\sigma$的高斯核卷积对octave3卷积，接着降采样得到octave4

• …

为什么要建这个金字塔呢？模拟摄像机拍摄的照片“近大远小”，远处的物体小，进出的物体大。高斯核去卷积模拟的是“近处清晰远处模糊”

高斯差分金字塔：

同一octave里，相邻的两层相减（就是普通的减法），得到DOG

高斯差分金字塔(DOG)

论文里建议，

octave组数的取值：

$O = \log_2(min(M,N)) - 3$，M,N是原图的宽和高

层数的取值：
$S = n+3$，n是希望提取的层数

尺度$\sigma$如何选择？

$$\begin{aligned} k &= 2^{\frac{1}{n}} \\ \sigma_0 &= \sqrt{1.6^2-0.5^2}=1.52 \end{aligned}$$

关键点位置的确定

1.阈值化

$$abs(val) > 0.5 \times \frac{T}{n}, T=0.04$$

ps：因为上一步是作的减法，所以可能会出现像素值为负数的情况。所以这里用了绝对值，T是自己设置的，在原始论文和opencv中都用的0.04。

如果这个绝对值太小，小于这个阈值的话，则认为该像素点是噪声，丢弃。

2.在高斯差分金字塔中找极值

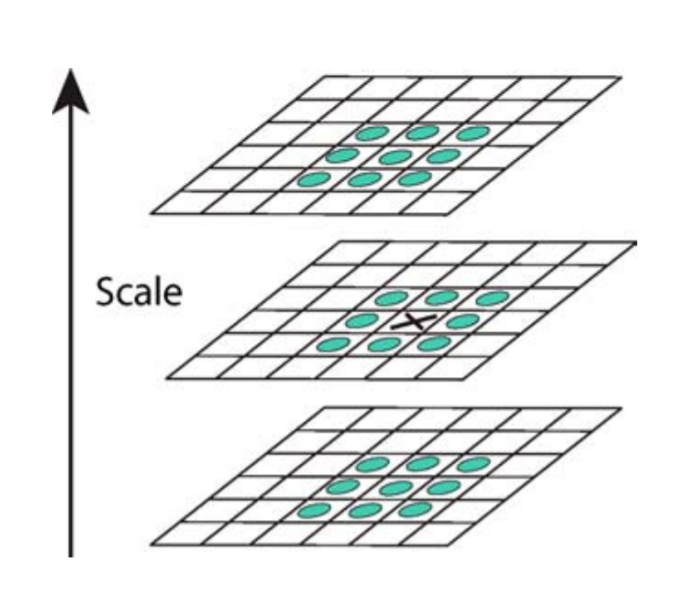
3.对极值点进行精确定位

上一步找到的极值点是离散空间中的极值点，因为尺度空间是离散的（上一层是下一层的k倍，中间的都没被取到，canny里用线性插值的方式去取，这里用泰勒展开）

在检测到极值点出做三元二阶泰勒展开

细节问题：迭代次数限制、解超出一定范围舍去

4. 舍去低对比度的点

若$|f(X)| < \frac{T}{n}$，则舍去点X

5. 边缘效应的去除

我这个小白：边缘效应是啥玩意儿？？？