本系列是记录与总结性质的文章，原创的内容少，记录的内容大都与考研有关。写博客的时间仓促，文中若有错误之处，恳请指正。

计算复杂度

以下内容几乎全部摘自《模式分类》[^1]

为了分析和描述某个问题或为解决为题而设计的某个特定算法的难度，我们转而讨论计算复杂度的概念。我们使用函数的阶这一概念，并且还使用渐进记号O\Omicron(大欧)，Ω(omega)\Omega (omega)和Θ(theta)\Theta (theta)。

渐进上界  O(g(x))={f(x)Ο(g(x)) = \{ f(x)：存在正的常数cc和x0x_0，对于所有的x≥x0x \geq x_0，有0≤f(x)≤cg(x)}0 \leq f(x) \leq cg(x) \}
渐进下界  Ω(g(x))={f(x)\Omega (g(x)) = \{ f(x)：存在正的常数cc和x0x_0，对于所有的x≥x0x \geq x_0，有0≤cg(x)≤f(x)}0 \leq cg(x) \leq f(x) \}
渐进紧界  Θ(g(x))={f(x)\Theta (g(x)) = \{ f(x)：存在正的常数c1c_1，c2c_2和x0x_0，对于所有的x≥x0x \geq x_0，有0≤c1g(x)≤f(x)≤c2g(x)}0 \leq c_1g(x) \leq f(x) \leq c_2g(x) \}
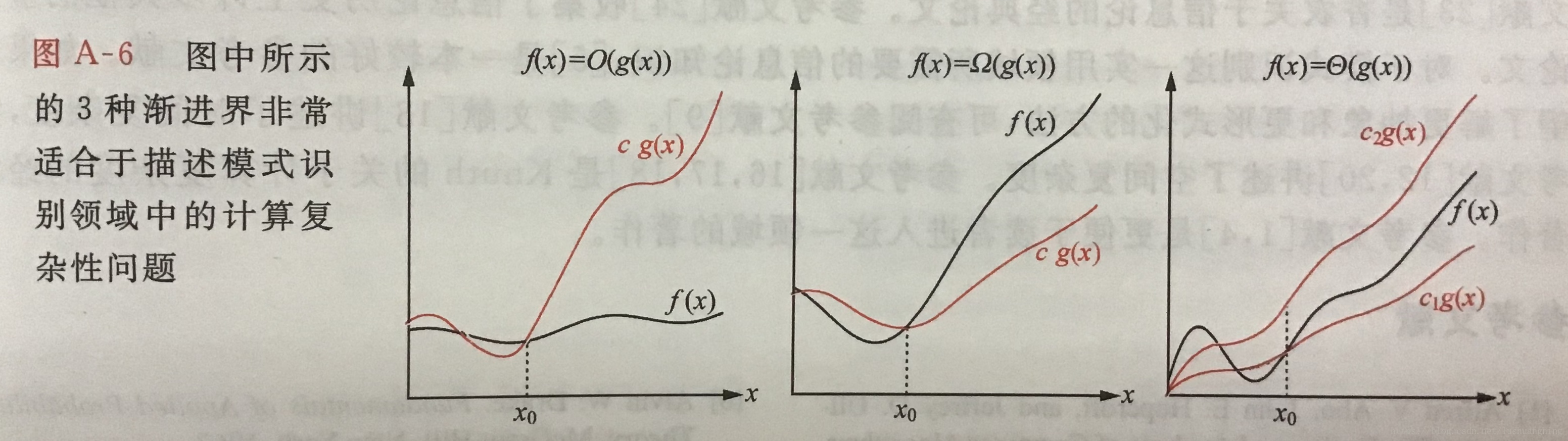
计算复杂性

例如，设f(x)=px2+mx+nf(x) = px^2 + mx + n，我们有f(x)=O(x2)f(x) = O(x^2)，因为对于足够大的xx，总可以选择恰当的c,x0c,x_0，使得px2+mx+n≤cx2px^2 + mx + n \leq cx^2。需要指出，对于函数f(x)f(x)，其渐进上界不是唯一的。对于f(x)=px2+mx+nf(x) = px^2 + mx + n，其渐进上界可以为O(x2),O(x3),O(x4),O(x2lnx)O(x^2),O(x^3),O(x^4),O(x^2ln x)，等等。

在计算复杂度中，渐进上界这一概念是所有的这些渐进边界中最有用的，因为通常情况下，我们都希望知道某个问题（或算法）耗时或占用内存的上限。

递归函数的时间复杂度

下面不加证明的给出递归函数的时间复杂度结论[^2]，如果想要了解完整的证明，请参考《算法导论》[^3]中的相关内容。不得不说，证明过程是相当复杂的。

分治法主定理

递归式是T(n)=aT(nb)+O(nklog⁡pn)T(n) = aT(\frac{n}{b}) + O(n^k \log^p n)，其中a≥1a \geq 1，b>1b > 1，k≥0k \geq 0且pp是实数，则：

  1. 如果a>bka > b^k，那么T(n)=O(nlog⁡ba)T(n) = O(n^{\log_b a})
  2. 如果a=bka = b^k
      a. 如果p>−1p > -1，那么T(n)=O(nlog⁡balog⁡p+1n)T(n) = O(n^{\log_b a} \log^{p+1} n)
      b. 如果p=−1p = -1，那么T(n)=O(nlog⁡balog⁡log⁡n)T(n) = O(n^{\log_b a} \log \log n)
      c. 如果p<−1p < -1，那么T(n)=O(nlog⁡ba)T(n) = O (n^{\log_b a})
  3. 如果a<bka < b^k
      a. 如果p≥0p \geq 0，那么T(n)=O(nklog⁡pn)T(n) = O(n^k \log^p n)
      b. 如果p<0p < 0，那么T(n)=O(nk)T(n) = O (n^k)

例题与分析

问题1    T(n)=3T(n2)+n2T(n) = 3T( \frac {n}{2}) + n^2
解答    T(n)=O(n2)T(n) = O(n^2)（根据主定理 3.a）

问题2    T(n)=4T(n2)+n2T(n) = 4T( \frac {n}{2}) + n^2
解答    T(n)=O(n2log⁡n)T(n) = O(n^2 \log n)（根据主定理 2.a）

问题3    T(n)=T(n2)+n2T(n) = T( \frac {n}{2}) + n^2
解答    T(n)=O(n2)T(n) = O(n^2)（根据主定理 3.a）

问题4    T(n)=2nT(n2)+nnT(n) = 2^nT( \frac {n}{2}) + n^n
解答    不适用（aa不是常数）

问题5    T(n)=16T(n4)+nT(n) = 16T( \frac {n}{4}) + n
解答    T(n)=O(n2)T(n) = O(n^2)（根据主定理 1）

问题6    T(n)=2T(n2)+nlog⁡nT(n) = 2T( \frac {n}{2}) + n \log n
解答    T(n)=O(nlog⁡2n)T(n) = O(n \log^2 n)（根据主定理 2.a）

问题7    T(n)=2T(n2)+nlog⁡nT(n) = 2T( \frac {n}{2}) + \frac {n}{\log n}
解答    T(n)=O(nlog⁡log⁡n)T(n) = O(n \log \log n)（根据主定理 2.b）

问题8    T(n)=2T(n4)+n0.51T(n) = 2T( \frac {n}{4}) + n^{0.51}
解答    T(n)=O(n0.51)T(n) = O(n^{0.51})（根据主定理 3.b）

问题9    T(n)=0.5T(n2)+1nT(n)=0.5T( \frac {n}{2}) + \frac {1}{n}
解答    不适用（a<1a<1）

问题10    T(n)=6T(n3)+n2log⁡nT(n) = 6T( \frac {n}{3}) + n^2 \log n
解答    T(n)=O(n2log⁡n)T(n) = O(n^2 \log n)（根据主定理 3.a）

问题11    T(n)=64T(n8)−n2log⁡nT(n) = 64T( \frac {n}{8}) - n^2 \log n
解答    不适用（函数值非正数）

问题12    T(n)=7T(n3)+n2T(n) = 7T( \frac {n}{3}) + n^2
解答    T(n)=O(n2)T(n) = O(n^2)（根据主定理 3.a）

问题13    T(n)=4T(n2)+log⁡nT(n) = 4T( \frac {n}{2}) + \log n
解答    T(n)=O(n2)T(n) = O(n^2)（根据主定理 1）

问题14    T(n)=16T(n4)+n!T(n) = 16T( \frac {n}{4}) + n!
解答    T(n)=O(n!)T(n) = O(n!)（根据主定理 3.a）

问题15    T(n)=2T(n2)+log⁡nT(n) = \sqrt{2}T( \frac {n}{2}) + \log n
解答    T(n)=O(n)T(n) = O(\sqrt{n})（根据主定理 1）

问题16    T(n)=3T(n2)+nT(n) = 3T( \frac {n}{2}) + n
解答    T(n)=O(nlog⁡3)T(n) = O(n^{\log 3})（根据主定理 1）

问题17    T(n)=3T(n3)+nT(n) = 3T( \frac {n}{3}) + \sqrt{n}
解答    T(n)=O(n)T(n) = O(n)（根据主定理 1）

问题18    T(n)=4T(n2)+cnT(n)=4T( \frac {n}{2}) +cn
解答    T(n)=O(n2)T(n) = O(n^2)（根据主定理 1）

问题19    T(n)=3T(n4)+nlog⁡nT(n) = 3T( \frac {n}{4}) + n \log n
解答    T(n)=O(nlog⁡n)T(n) = O(n \log n)（根据主定理 3.a）

问题20    T(n)=3T(n3)+n2T(n) = 3T( \frac {n}{3}) + \frac {n}{2}
解答    T(n)=O(nlog⁡n)T(n) = O(n \log n)（根据主定理 2.a）

问题规模减小的递归主定理

令T(n)T(n)为正整数nn的函数，对于某些常数c,a>0,b>0,k≥0c,a > 0,b > 0,k \geq 0和函数f(n),T(n)f(n),T(n)满足下面的性质：

T(n)={cn≤1aT(n−b)+f(n)n>1T(n) = \begin{cases} c & n \leq 1 \\ aT(n-b) + f(n) & n > 1 \end{cases}

如果f(n)f(n)的时间复杂度是O(nk)O(n^k)，则

T(n)={O(nk)a≤1O(nk+1)a=1O(nkanb)a>1T(n) = \begin{cases} O(n^k) & a \leq 1 \\ O(n^{k+1}) & a = 1 \\ O(n^ka^ \frac{n}{b}) & a > 1 \end{cases}

循环的时间复杂度

数学基础

前nn项和公式

∑k=1nk=n(n+1)2\sum_{k=1}^n k = \dfrac{n(n+1)}{2}

平方和公式

∑k=1nk2=n(n+1)(2n+1)6\sum_{k=1}^n k^2 = \dfrac{n(n+1)(2n+1)}{6}

立方和公式

∑k=1nk=n2(n+1)24\sum_{k=1}^n k = \dfrac{n^2(n+1)^2}{4}

例题与分析

1
2
3
4
5
6
7
for(int i=1; i <= n; i++){
	for(int j=1; j<= i; j++){
		for(int k=1; k <=j; k++){
			//do something
		}
	}
}

T(n)=∑i=1n∑j=1i∑k=1j1=∑i=1n∑j=1ij=∑i=1ni(i+1)2=12[n(n+1)(2n+1)6+n(n+1)2]=O(n3)\begin{aligned} T(n) & = \sum_{i=1}^n \sum_{j=1}^i \sum_{k=1}^j 1 = \sum_{i=1}^n \sum_{j=1}^i j = \sum_{i=1}^n \frac{i(i+1)}{2} \\ & = \dfrac{1}{2} [ \frac {n(n+1)(2n+1)}{6} + \frac {n(n+1)}{2}] = O(n^3) \end{aligned}

参考书籍

  1. （美）Richard O.Duda, Peter E.Hart, David G.Stork.模式分类（原书第2版）[M].李宏东, 姚天翔等, 译.北京：机械工业出版社.2003.

  2. （印度）Narasimha Karumanchi.数据结构与算法经典问题解析（原书第2版）[M].骆嘉伟等，译.北京：机械工业出版社.2016.

  3. （美）Thomas H.Cormen, Charles E.Leiserson, Ronald L.Rivest等，著.算法导论（原书第3版）[M].殷建平，徐云，王刚等，译.北京：机械工业出版社.2013.