写在前面

本系列是记录与总结性质的文章，原创的内容少，记录的内容与计算机考研有关。在考研的范畴里，与树相关的算法很多，在程序设计题中属于必考题。我准备用三篇博客来总结与树有关的算法。

数据结构的定义和规范参考严书^1 和王道^2。前一本是很多高校的指定参考书，后一本是考研辅导书。

最后，由于写博客的时间仓促，文中若有错误之处，恳请朋友们批评指正。

工具

在考试中，实现树的相关算法时很可能会用到栈或队列，可以直接把他们作为一个工具来解决问题。即，把栈或队列的声明和操作写得很简单，不必分函数写出。以顺序栈的操作为例：
(1) 声明一个栈并初始化：

1
2
3

//下面两句连声明带初始化都有了
ElemType stack[maxSize];
int top = -1;

(2)元素进栈

1	stack[++top] = x; //仅一句话即实现进栈操作

(3)元素x出栈

1	x = stack[top--];

更简单的，可以直接使用栈和队列的基本操作的函数来实现操作。栈的基本操作有：

InitStack(S);	//初始化

StackEmpty(S);	//判空

Push(S,x);	//元素x进栈

Pop(S,x);	//栈顶元素出栈并赋值给x

GetTop(S,x);	//读栈顶元素并赋值给x

相应的，队列的基本操作如下：

InitQueue(Q);	//初始化队列

QueueEmpty(Q);	//判空

EnQueue(Q,x);	//元素x入队

DeQueue(Q,x);	//出队，赋值给x

GetHead(Q,x);	//读队头元素，赋值给x

二叉树的遍历

二叉链表的定义

typedef struct BiTNode{
    ElemType data;
    struct BiTNode * lchild, * rchild;
}BiTNode, * BiTree;

二叉树的遍历，递归算法写起来非常简单。重点在与如何用非递归算法来实现遍历。

递归实现

1.先序遍历（PreOrder）

void PreOrder(BiTree T){
    if(T != NULL){
        visit(T);
        PreOrder(T->lchild);
        PreOrder(T->rchild);
    }
}

时间复杂度： $O(n)$
空间复杂度：最差 $O(n)$ ，平均 $O(logn)$

2.中序遍历（InOrder）

void InOrder(BiTree T){
    if(T != NULL){
        InOrder(T->lchild);
        visit(T);
        InOrder(T->rchild);
    }
}

3.后序遍历（PostOrder）

void PostOrder(BiTree T){
    if(T != NULL){
        PostOrder(T->lchild);
        PostOrder(T->rchild);
        visit(T);
    }
}

非递归实现

1.先序遍历

void PreOrder2(BiTree T){
    BiTree p = T;

    InitStack(S);	//初始化一个空栈

    if(p != NULL){
        Push(S,p);  //结点进栈
        while(!StackEmpty(S)){
            Pop(S,p);  //出栈，赋值给p
            visit(p);

            if(p->rchild){	//一定是右孩子先入栈
                Push(S,p-rchild);
            }

            if(p->lchild){
                Push(S,p->lchild);
            }
        }
    }
}

2.中序遍历

void InOrder2(BiTree T){
    BiTree = T;

    InitStack(S);
    while(p || !StackEmpty(S)){
        if (p != NULL){
            Push(S,p);
            p = p->lchild;
        }else{
            Pop(S,p);
            visit(p);
            p = p->rchild;
        }
    }
}

3.后序遍历（重点难点）

void PostOrder2(BiTree T){
    InitStack(S);
    BiTree p = T;
    BiTree r = NULL;

    while(p || !IsStackEmpty(S)){
        if(p){
            Push(S,p);
            p = p->lchild;
        }else{
            GetTop(S,p);
            if(p->rchild && p->rchild != r){
                p = p->rchild;
                Push(S,p);
                p = p->lchild;
            }else{
                Pop(S,p);
                visit(p);
                r = p;
                p = NULL;
            }
        }
    }
}

之所以说后序遍历的非递归算法是重点难点，是因为每当访问一个结点x时，此时栈里存储的元素正好是x的所有祖先。后面的题目里求叶子结点的所有祖先，或者输出根到叶子的路径，都和这个非递归的后序遍历紧密相关。

4.层次遍历

void LevelOrder(BiTree T){
    BiTree p;

    InitQueue(Q);
    EnQueue(Q,T);  //根节点入队

    while(!QueueEmpty(Q)){
        DeQueue(Q,p);  //出队，赋值给p
        visit(p);
        if(p->lchild){
            EnQueue(Q,p->lchild);
        }
        if(p->rchild){
            EnQueue(Q,p->rchild);
        }
    }
}

特殊实现

Morris 方法

初始时令 curr 指向根

规则：

curr 左子树不为空，找到左子树中最右侧的结点 most_right；
    * most_right 的右指针为空，most_right->right = curr;
    curr = curr->left;
    * most_right 的右指针指向 curr，most_right->right = nullptr;
    curr = curr->right;

左子树为空，`curr = curr->right;`

curr 出现的顺序，称为 Morris 序

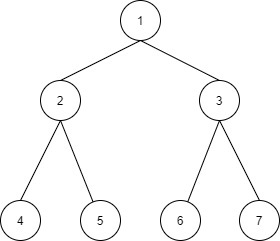
该树的 Morris 序为：

1,2,4,2,5,1,3,6,3,7

规律：

1
2
3

无左树的结点，Morris 序里一定只出现一次；
有左树的结点，Morris 序里一定出现两次；
有左树的结点，在第二次出现之前，一定会把左树都遍历完；

该方法在不使用栈的情况下，使用空闲指针建立了一种回到上一级的机制。可以利用左树上最右孩子的右指针来判断是第几次出现。

先序：保存Morris序第一次出现的结点
中序：只能够来到自己一次的结点，直接保存；能来到自己两次的结点（只要有左子树，必然能回到自己两次），保存第二次（通过左子树最右结点右指针的指向，知道是第几次）；
后序：